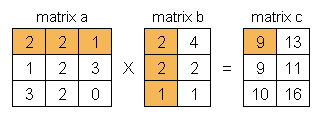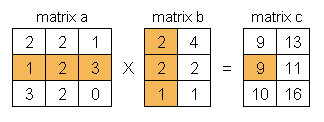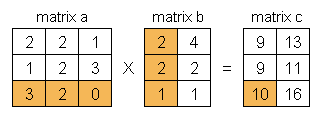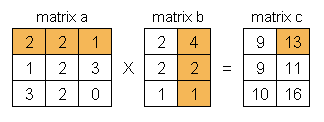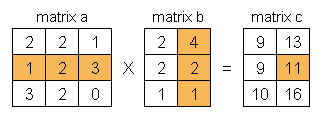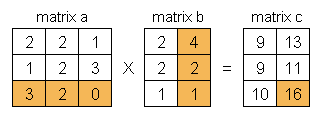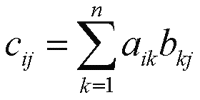Perkalian Matriks

Seseorang mengirim email kepada saya. Bertanya bagaimana cara perkalian matriks dengan bahasa php? Baiklah, saya akan mencoba memberi jawaban dengan batas kemampuan saya. Lalu terbersit ide, mengapa tidak dimuat saja di situs ini? Jadi bisa memberi manfaat bagi yang lainnya, dan tentu saja untuk sang penanya sendiri.

Sebagai gambaran dari proses perkalian matriks, silahkan lihat diagram. Diagram menggambarkan perkalian matriks dengan cara yang umumnya digunakan. Untuk mengalikan matriks a dengan matriks b, maka jumlah kolom matriks a harus sama dengan jumlah baris matriks b. Pada contoh ini matriks a mempunyai 3 kolom, dan matriks b mempunyai 3 baris.

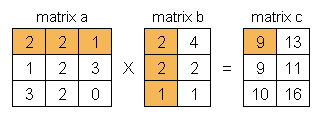
Diagram pertama ini menunjukkan, untuk mendapatkan elemen c_1,1 persamaannya adalah :
c_1,1 = (a_1,1 x b_1,1) + (a_1,2 x b_2,1) + (a_1,3 x b_3,1)
Dengan penulisan indeks c_x,y, dimana x adalah baris, dan y adalah kolom. Contoh ini, bila diganti dengan angka yang ada dalam matriks tersebut menjadi :
9 = (2 x 2) + (2 x 2) + (1 x 1)
Demikian seterusnya untuk mendapatkan hasil perkalian matriks a dan matriks b, lihat dalam urutan diagram berikut ini.

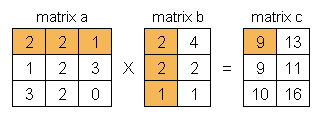
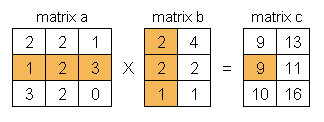
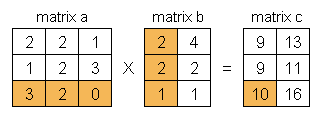
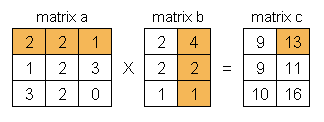
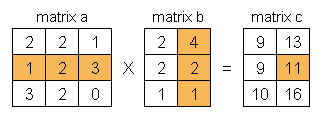
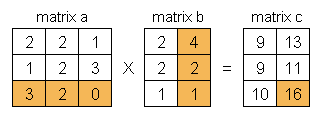
Apabila ditulis dengan rumus matematika yang agak serius :) maka perkalian matriks ditulis seperti berikut

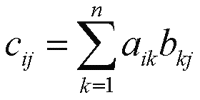
Dimana i adalah indeks untuk baris, j indeks untuk kolom, dan n adalah jumlah kolom matriks a.

Untuk melakukan proses perkalian matriks dengan menggunakan bahasa pemrograman tertentu, kita bisa mengikuti cara (algoritma) yang berlaku di atas. Proses ini melibatkan struktur data berbentuk array, loop, dan operasi perkalian, serta penjumlahan.

Pertama, inisialisasi dulu matriks yang akan dikalikan. Matriks a dan matriks b yang akan dikalikan diisi terlebih dahulu dengan nilai yang diinginkan. Sedangkan matriks c yang merupakan hasil dari perkalian kedua matriks ini, semua eloemennya diinisialisasi dengan nilai 0. Array yang digunakan untuk matriks adalah array 2 dimensi. Setelah inisialisasi data, proses perkalian matriks sudah bisa dilakukan. Dan berikutnya, jika diperlukan, tampilkan hasil perkalian.

Proses perkalian matriks dilakukan dengan menggunakan loop, seperti berikut ini :

for ($j = 1; $j <= $kolom_matriks_b; $j++) {
  for ($i = 1; $i <= $baris_matriks_a; $i++) {
    for ($k = 1; $k <= $kolom_matriks_a; $k++) {
      $c[$i][$j] = $c[$i][$j] + ($a[$i][$k] * $b[$k][$j]);
    }
  }
}

Loop dengan indeks $j akan melakukan perulangan sebanyak jumlah kolom matriks b. Kemudian loop di dalamnya dengan indeks $i, akan melakukan perulangan sebanyak jumlah baris matriks a. Dan terahir, loop terdalam dengan indeks $k akan melakukan perulangan sebanyak jumlah kolom matriks a.

Jika dilihat operasi yang ada dalam loop terdalam, yaitu :

      $c[$i][$j] = $c[$i][$j] + ($a[$i][$k] * $b[$k][$j]);

sama dengan bentuk rumus perkalian matriks di atas.

Dan berikutnya, saya memang kesulitan menguraikan proses perkalian matriks dengan bahasa program pada contoh ini. Walaupun proses ini hanya 7 baris, bisa jadi jika diurai dengan kata-kata menjadi begitu panjang rasanya. Jadi, maafkan saya. Mudah-mudahan saja dengan menulis diagram, dan contoh ini, bisa membantu dalam memahami perkalian matriks menggunakan sebuah bahasa pemrograman.

Saya menyertakan dua buah script php yang melakukan proses perkalian matriks. Contoh pertama menggunakan data yang sudah tertentu nilainya. Sedangkan contoh kedua dengan memanfaatkan data random, sehingga matriks yang ditampilkan bisa berbeda-beda. Sebagai info, script saya jalankan pada php versi 4.3.10 Silahkan klik pada link berikut untuk melihat source code contoh tersebut.

Contoh 1    Contoh 2

Untuk tambahan, jika kita lihat algoritma di atas, berapakah kompleksitasnya? Dari pengamatan sekilas, dengan menggunakan loop sampai kedalaman 3, bisa jadi berbentuk n³. Dengan asumsi bahwa matriks a dan matriks b adalah matriks bujursangkar (n x n), maka perhitungan kompleksitas secara sederhana seperti berikut :

• Proses terdalam c = c + (a x b) memerlukan proses tambah dan kali, dilakukan sebanyak jumlah kolom matriks a, yaitu n. Jadi proses ini memerlukan 2n langkah
• Karena proses ini berada dalam loop di luarnya sebanyak jumlah baris matriks a (sebanyak n), maka langkah sebanyak 2n tadi menjadi 2n x n = 2n²
• Dan masih ada satu loop di luarnya yang dilakukan sebanyak jumlah kolom matriks b (sebanyak n), maka 2n² x n = 2n³

Jadi secara kasar, memang kompleksitas dengan algoritma ini berorde 3. Dan tentu saja ini perlu sedikit perhatian. Misalnya dengan matriks 2 x 2, kita memerlukan langkah sebanyak 2³ = 8. Dan ketika dengan matriks 5 x 5, diperlukan 5³ = 125 langkah. Dan ketika dengan matriks 10 x 10, diperlukan 10³ = 1000 langkah. Dan jika dengan matriks 100 x 100, diperlukan 100³ = 1000000 langkah!